一道小学一年级寒假数学题

qyb 发表于 2010-01-28 21:19:03

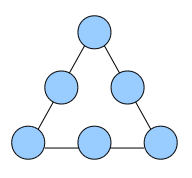
把 2,3,4,5,6,7 六个数，填入如下图的空中，要求每条边三个数的和相等

是不是已经有点夸张了？

但更雷人的是要找出3种不同的方案！！（对于以为滚一滚就能弄出三种方案的同志，我得提示一下，应该是有4种方案的——三边之和分别是 12/13/14/15）

这个我就觉得完全超出了一个7岁儿童的思维能力...我相信就算是一个成年人，没有经过对数字敏感度的训练，也无从下手呢.

Topic: dada

评论

Hetty (未验证) 在 Thu, 2010-01-28 22:11 提交

可以凑一凑，然后再滚一滚
个人觉得，并不需要对数字太敏感
也可以用奇妙的方式通向答案的

小孩子在这方面尤其厉害也说不定

Anonymous (未验证) 在 Thu, 2010-01-28 23:02 提交

嘻嘻，4种俺都算出来了

cloudzhou (未验证) 在 Fri, 2010-01-29 10:02 提交

假设从一个顶角节点沿同一个方向遍历，所遍历的数字为 a1 a2 a3 a4 a5 a6
长度 l = a1+a2+a3 = a3+a4+a5 = a5+a6+a1
那么有
l = (a1+a2+a3 + a3+a4+a5 + a5+a6+a1)/3
= (a1 + a2 + a3 + a4 + a5 + a6 + a1 + a3 + a5)/3
= (a1 + a2 + a3 + a4 + a5 + a6)/3 + (a1 + a3 + a5)/3
那么对于本题，(a1 + a2 + a3 + a4 + a5 + a6)/3 = 9
最短的边是
9 + (2+3+4)/3 = 12
最长的边是
9 + (5+6+7)/3 = 15
所以边长可以尝试使用 12 13 14 15，并且每个顶角节点都是确定的，然后再尝试添数字

如何？

qyb 在 Fri, 2010-01-29 10:15 提交

恭喜你，可以去上小学一年级了..

我的做法是，首先尝试在三个顶点写上2,3,4，很容易发现剩下三个空怎么填。。得到12

随即，在三个顶点写下5,6,7，这就得到了15

那么怎么去找第三种方案呢？我注意到上述两个方案的本质是把这6个数分成了两组等差数列填空，于是分出了 2/4/6和3/5/7，剩下两个方案搞定..

以上解题过程不到1分钟

cloudzhou (未验证) 在 Fri, 2010-01-29 10:28 提交

我倒是在想，如果这个话题扩充为一个计算机算法的问题，
可以有a1,a2,...a(n-1),a(n)个数，
然后有一个等边三角形，其中顶角节点共用，然后每个边长有m个节点
其中 m*3 - 3 = n

那么要求能够列举出所有的符合本题条件的边长的组合

请问如何做 :)

如果我能想出来，我再来回复

cloudzhou (未验证) 在 Fri, 2010-01-29 10:35 提交

我觉得小孩子做这样的题目是有好处的，即使使用的是“暴力破解”，还是能锻炼小孩的数字敏感性

allan (未验证) 在 Mon, 2010-02-01 21:51 提交

我认为小孩子的做法应该是吧数字填到不同的边然后剩下的去试

est (未验证) 在 Fri, 2010-01-29 11:43 提交

我觉得把数学算术化才是中国教育的悲哀。

qyb 在 Fri, 2010-01-29 14:07 提交

反正生小孩之前，得三思... 万恶的旧社会